Table of contents

Matrix construction in 𝓗𝖫𝖨𝖡𝗉𝗋𝗈 is the processor of using a given block cluster tree 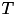$ T $ and constructing matrices for all leaves in 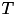$ T $ and for all inner nodes of 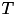$ T $ . The leaf matrices define the actual content of the matrix and may be of various formats, e.g. dense (TDenseMatrix) and low rank (TRkMatrix) matrices . Inner nodes on the other hand define the hierarchy of the 𝓗-matrix and are important for the matrix algebra. Such block matrices are usually of type TBlockMatrix.

A special version of a block matrix is THMatrix, which also stores the permutations supplied by block cluster trees to map between internal and external ordering of the unknowns during matrix vector multiplication. Standard block matrices, e.g. of type TBlockMatrix, will only know about the interal ordering of unknowns.

Remarks: This mapping is only supported for matrix vector multiplication and not for general matrix algebra.

All matrix construction techniques are derived from the corresponding base class TMatBuilder, which defines the basic build interface, which mainly consists of the function build:

virtual TMatrix * build ( const uint                nthreads,
                          const TBlockClusterTree * cluster,  // ← full tree
                          const TTruncAcc &         acc,
                          TProgressBar *            progress = NULL ) const;
virtual TMatrix * build ( const uint                nthreads,
                          const TBlockCluster *     cluster,  // ← sub tree
                          const TTruncAcc &         acc,
                          TProgressBar *            progress = NULL ) const;

Both functions will construct 𝓗-matrices as described above using nthreads parallel threads and with a local accuracy defined by acc. Furthermore, a progress meter may be supplied to indicate the current state of the process.

The difference between both functions comes from the different type of cluster. In the first case a TBlockClusterTree object is given and thereby also the mappings between internal an external ordering of the unknowns stored within this object. This allows the construction of a THMatrix object. In the second case, this information is not available and therefore (usually) a TBlockMatrix object will be returned.

Dense Matrices

In a dense matrix 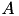$ A $ , all leaf nodes of the block cluster tree will usually be represented by a non-zero matrix block. By default, a non-admissible leaf node will become a dense matrix, e.g. TDenseMatrix, and an admissible node will become a low rank matrix, e.g. TRkMatrix. This construction is implemented in TDenseMBuilder, which needs two additional object to perform the 𝓗-matrix construction:

a coefficient function, which returns the actual matrix coefficients of 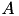for a given sub block of the matrix and
a low rank approximation object, which will construct low rank approximations of sub blocks of .

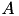Coefficient Functions

The coefficient function has to be of type TCoeffFn or, to be precise of a derived class (as TCoeffFn is abstract). The main function in TCoeffFn is:

virtual void eval  ( const TIndexSet &  rowis,
                     const TIndexSet &  colis,
                     value_t *          matrix ) const;

Here, value_t is either real or complex and defined in the form of a template argument to TCoeffFn. The function is given a block index set rowis × colis for which the coefficients should be stored in matrix. Hereby, matrix has to be access column wise (as usual in 𝓗𝖫𝖨𝖡𝗉𝗋𝗈) such that the coefficient corresponding to the i'th index in row and to the j'th index in colis has to be stored at position (i,j) in matrix, e.g.:

const size_t  nrows = rowis.size();
const size_t  ncols = colis.size();
for ( size_t  j = 0; j < ncols; ++j ) {
    const idx_t  col_idx = colis.first() + j;
    for ( size_t  i = 0; i < nrows; ++i ) {
        const idx_t  row_idx = rowis.first() + i;
        const real   f        = ... // compute coefficient (row_idx,col_idx)
        matrix[ j * nrows + i ] = f;
    }
}

In most applications the indices supplied by rowis and colis have to be mapped to the external indices. To ease the implementation of coefficient functions in such cases, TPermCoeffFn is available in 𝓗𝖫𝖨𝖡𝗉𝗋𝗈. Here, the mapping is already performed and a new version of eval is called:

virtual void  eval   ( const std::vector< idx_t > &  rowis,
                       const std::vector< idx_t > &  colis,
                       value_t *                     matrix ) const;

Instead of the TIndexSet objects in the previous case, which correspond the consecutively numbered index sets, these functions will be called with the actual index sets in external ordering (which are usually in arbitrary order). Beside this difference, the access of matrix follows the same scheme:

const size_t  nrows = tau.size();
const size_t  ncols = sigma.size();
for ( size_t  j = 0; j < ncols; ++j ) {
    const idx_t  col_idx = colis[j];
    for ( size_t  i = 0; i < nrows; ++i ) {
        const idx_t  row_idx = rowis[i];
        const real   f        = ... // compute coefficient (row_idx,col_idx)
        matrix[ j * nrows + i ] = f;
    }
}

TPermCoeffFn should also be considered being a base class for derived coefficient functions as it only defines the interface for the coefficient evaluation, not the actual computation.

Another property of the final 𝓗-matrix has to be defined by the coefficient function, namely the matrix format, e.g. whether it is unsymmetric, symmetric or hermitian. This is done by overloading the function

virtual matform_t matrix_format () const;

A full example for a user defined cofficient function is described in Solving an Integral Equation.

Low Rank Approximation

𝓗𝖫𝖨𝖡𝗉𝗋𝗈 provides several techniques for computing low rank approximations for dense matrices:

TSVDLRApx: singular value decomposition,
TACA: classical adaptive cross approximation (ACA),
TACAPlus: advanced ACA with additional tests,
TACAFull: ACA with full pivoting,
THCA: hybrid cross approximation (HCA),
TZeroLRApx: approximate by 0, e.g. build just nearfield.

Although singular value decomposition will compute the best approximation, it is also the most time consuming with a computational complexity of 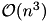$\mathcal{O}(n^3)$ , where 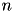$ n $ is the number of rows/columns.

ACA is a heuristical approximation technique based on consecutive elimination of rank-1 matrices. In contrast to the HCA will always return an approximation of a given accuracy. The advantage of ACA compared to HCA is, that it only needs access to the matrix coefficients, whereas HCA needs further functionality, e.g. evaluation of collocation integrals. Both, ACA and HCA have a runtime of 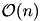$\mathcal{O}(n)$ . ACA-Full is a special variant of ACA where the full matrix is searched for the best rank-1 matrix to eliminate. 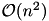This also guarantees the wanted accuracy albeit with a higher complexity ( $\mathcal{O}(n^2)$ ).

Remarks: Except when problems are known, TACAPlus will work in most applications and should therefore be the default choice.

Solving an Integral Equation contains a complete example for 𝓗-matrix construction based on dense matrices.

Sparse Matrices

Representing sparse matrices using 𝓗-matrices will usually result in a much higher memory consumption since 𝓗-matrices have move overhead in storing data. Hence, it should only be performed if additional arithmetic is wanted for these matrices. The standard case is the computation of an 𝓗-LU factorisation of a sparse matrix.

The construction of the leaf matrix blocks, and hence, the construction of the 𝓗-matrix out of a sparse matrix is done by TSparseMBuilder. Beside the actual sparse matrix, it expects also mappings for the row and the column index sets between internal and external ordering since the sparse matrix is often given in external ordering. If not, the mappings may be NULL.

TSparseMBuilder   builder( S, ct->perm_i2e(), ct->perm_e2i() );
A = builder.build( 1, bct.get(), acc );

A complete example for 𝓗-matrix construction with sparse matrices can be found in Solving a Sparse Equation System.

Remarks: In most applications admissible blocks will be zero in the resulting 𝓗-matrix since only for neighboured (geometrically or algebraically) indices, and hence for the nearfield, non-zero coefficients will occur.

A special mode can be activated within TSparseMBuilder where instead of using TDenseMatrix and TRkMatrix, all leaf matrices will be constructed as sparse matrices itself. Although this significantly reduces the memory consumption of the final 𝓗-matrix, no arithmetic is supported for such a matrix beside matrix-vector multiplication. This mode can be enabled/disable by calling set_sparse_mode:

TSparseMBuilder   builder( S, NULL, NULL );
builder.set_sparse_mode( true );  // enable sparse leaf matrices
A = builder.build( 1, bct.get(), acc );