Functions |
| void | eval_diag (const TMatrix *A, TVector *v, const matop_t op, const tri_eval_option_t &options) |
| | evaluate D·x=y with (block) diagonal D
|
| void | eval (const TMatrix *A, TVector *v, const matop_t op, const tri_eval_option_t &options) |
| | evaluate L·U·x=y with lower triangular L and upper triangular U
|
| void | eval_lower (const TMatrix *A, TVector *v, const matop_t op, const tri_eval_option_t &options) |
| | evaluate A·x=y with lower triangular A
|
| void | eval_upper (const TMatrix *A, TVector *v, const matop_t op, const tri_eval_option_t &options) |
| | evaluate A·x = y with upper triangular A
|
| void | invert (const uint nthreads, TMatrix *A, const TTruncAcc &acc, const inv_options_t opts=inv_options_t()) |
| | compute 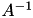
|
|
void | invert (TMatrix *A, const TTruncAcc &acc, const inv_options_t opts=inv_options_t()) |
| | compute 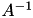 (sequential version) (sequential version)
|
| TVector * | inverse_diag (const uint nthreads, TMatrix *A, const TTruncAcc &acc, const inv_options_t opts=inv_options_t()) |
| | Compute diagonal of 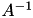 . .
|
|
void | multiply_diag (const uint nthreads, const real alpha, const matop_t op_A, const TMatrix *A, const matop_t op_D, const TMatrix *D, const matop_t op_B, const TMatrix *B, const real beta, TMatrix *C, const TTruncAcc &acc, TProgressBar *progress=NULL) |
| | compute C ≔ β·C + α·op(A)·op(D)·op(B) where D is a block diagonal matrix
|
|
size_t | multiply_diag_steps (const matop_t op_A, const TMatrix *A, const matop_t op_D, const TMatrix *D, const matop_t op_B, const TMatrix *B, const TMatrix *C) |
| | return number of steps for computing C ≔ C + op(A)·op(D)·op(B)
|
|
void | mul_diag_left (const TScalarVector &v, TMatrix *A) |
| | compute B = diag(v)·A and overwrite A
|
|
void | mul_diag_right (TMatrix *A, const TScalarVector &v) |
| | compute B = A·diag(v) and overwrite A
|
Matrix Addition |
Functions for matrix addition
|
| void | add (const uint nthreads, const real alpha, const TMatrix *A, const real beta, TMatrix *C, const TTruncAcc &acc) |
| | C ≔ α·A + β·C.
|
| void | cadd (const uint nthreads, const complex &alpha, const TMatrix *A, const complex &beta, TMatrix *C, const TTruncAcc &acc) |
| | C = α·A + β·C.
|
|
void | add_identity (TMatrix *A, const real lambda) |
| | compute A ≔ A + λ·I
|
|
void | cadd_identity (TMatrix *A, const complex lambda) |
| | compute A ≔ A + λ·I
|
Matrix Factorisation |
Functions related to matrix factorisation, e.g. LU or Cholesky factorisation.
|
| TMatrix * | factorise (const uint nthreads, TMatrix *A, const TTruncAcc &acc, const fac_options_t &options=fac_options_t()) |
| | compute factorisation of A
|
| TMatrix * | factorise_inv (const uint nthreads, TMatrix *A, const TTruncAcc &acc, const fac_options_t &options=fac_options_t()) |
| | compute factorisation of A and return inverse operator
|
|
void | lu (const uint nthreads, TMatrix *A, const TTruncAcc &acc, const fac_options_t &options=fac_options_t()) |
| | compute LU factorisation using TLU
|
|
void | ldu (const uint nthreads, TMatrix *A, const TTruncAcc &acc, const fac_options_t &options=fac_options_t()) |
| | compute LDU factorisation using TLDU
|
|
void | ll (const uint nthreads, TMatrix *A, const TTruncAcc &acc, const fac_options_t &options=fac_options_t()) |
| | compute LL^H factorisation using TLL
|
|
void | ldl (const uint nthreads, TMatrix *A, const TTruncAcc &acc, const fac_options_t &options=fac_options_t()) |
| | compute LDL^H factorisation using TLDL
|
Matrix Multiplication |
Functions for matrix multiplication.
|
| void | multiply (const uint nthreads, const real alpha, const matop_t op_A, const TMatrix *A, const matop_t op_B, const TMatrix *B, const real beta, TMatrix *C, const TTruncAcc &acc, TProgressBar *progress=NULL) |
| | compute C ≔ β·C + α·op(A)·op(B)
|
| void | cmultiply (const uint nthreads, const complex alpha, const matop_t op_A, const TMatrix *A, const matop_t op_B, const TMatrix *B, const complex beta, TMatrix *C, const TTruncAcc &acc, TProgressBar *progress=NULL) |
| | compute C ≔ β·C + α·op(A)·op(B) using nthreads
|
|
void | multiply (const uint nthreads, const real alpha, const TMatrix *A, const TMatrix *B, const real beta, TMatrix *C, const TTruncAcc &acc, TProgressBar *progress=NULL) |
| | compute C = β·C + α·A·B using nthreads
|
|
void | multiply (const real alpha, const TMatrix *A, const TMatrix *B, const real beta, TMatrix *C, const TTruncAcc &acc, TProgressBar *progress=NULL) |
| | compute C = β·C + α·A·B sequentially
|
|
void | cmultiply (const uint nthreads, const complex alpha, const TMatrix *A, const TMatrix *B, const complex beta, TMatrix *C, const TTruncAcc &acc, TProgressBar *progress=NULL) |
| | compute C = β·C + α·A·B using nthreads
|
|
void | cmultiply (const complex alpha, const TMatrix *A, const TMatrix *B, const complex beta, TMatrix *C, const TTruncAcc &acc, TProgressBar *progress=NULL) |
| | compute C = β·C + α·A·B sequentially
|
|
size_t | multiply_steps (const matop_t op_A, const TMatrix *A, const matop_t op_B, const TMatrix *B, const TMatrix *C) |
| | return number of steps for computation of C ≔ C + op(A)·op(B) for progress meter initialisation
|
Matrix-Vector Multiplication |
Functions for (parallel) matrix-vector multiplication
|
| void | mul_vec (const TProcSet &ps, const real alpha, const TMatrix *A, const TVector *x, const real beta, TVector *y, const matop_t op) |
| | compute y ≔ α·A·x + β·y on (possibly) distributed matrix A on all processors in ps
|
| void | cmul_vec (const TProcSet &ps, const complex alpha, const TMatrix *A, const TVector *x, const complex beta, TVector *y, const matop_t op) |
| | same as mul_vec but with complex valued scalars (
|
This module provides most higher level algebra functions, e.g. matrix multiplication, inversion and factorisation. See also Basic Matrix Algebra and Matrix Factorisation for an introduction into 𝓗-arithmetic.
to your source files.
| TMatrix* HLIB::factorise |
( |
const uint |
nthreads, |
|
|
TMatrix * |
A, |
|
|
const TTruncAcc & |
acc, |
|
|
const fac_options_t & |
options = fac_options_t() |
|
) |
| |
Compute triangular factorisation of A while choosing appropriate factorisation method depending on the format of A, e.g. if unsymmetric, symmetric or hermitian.
The return value is a matrix object representing the factorised form and suitable for evaluation, e.g. matrix-vector multiplication (see TFacMatrix). A will be overwritten with the actual factorisation data.
| void HLIB::multiply |
( |
const uint |
nthreads, |
|
|
const real |
alpha, |
|
|
const matop_t |
op_A, |
|
|
const TMatrix * |
A, |
|
|
const matop_t |
op_B, |
|
|
const TMatrix * |
B, |
|
|
const real |
beta, |
|
|
TMatrix * |
C, |
|
|
const TTruncAcc & |
acc, |
|
|
TProgressBar * |
progress = NULL |
|
) |
| |
The function computes to matrix product \form#19
where \form#20 and \form#21 may be the non-modified, transposed or adjoint
matrices \form#3 and \form#22 respectively.
The result of the multiplication is written to \form#23, whereby the block structure
of \a C is not changed, e.g. the resulting block structure of the product is defined
by \a C.
Thread-parallel execution is supported by the matrix multiplication.
This function is available in various versions without corresponding parameters, e.g.
without \a op_A, \a op_B or without \a nthreads.
- Parameters
-
| nthreads | set number of threads to use |
| alpha | scaling factor of product |
| op_A | matrix modifier for A |
| A | first matrix factor |
| op_B | matrix modifier for B |
| B | second matrix factor |
| beta | scaling factor for C |
| C | matrix to update |
| acc | accuracy of multiplication |
| progress | optional progress bar |
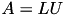 . More...
. More...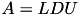 . More...
. More...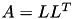 or
or 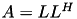 More...
More...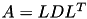 or
or 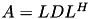 More...
More...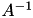
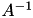 (sequential version)
(sequential version) 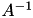 .
. 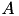 with block-wise accuracy acc and by using up to nthreads threads. A is overwritten by
with block-wise accuracy acc and by using up to nthreads threads. A is overwritten by 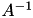 during inversion.
during inversion.  1.8.1.2
1.8.1.2