Table of contents

In this example, an integral equation is to be solved by representing the discretised operator with an 𝓗-matrix, whereby the 𝓗-matrix is constructed using a matrix coefficient function for entries of the equation system. Furthermore, for the iterative solver a preconditioner is computed using 𝓗-LU factorisation.

Problem Description

Given the integral equation

$\begin{displaymath} \int_0^1 \log|x-y| \mathbf{u}(y) dy = \mathbf{f}(x), \quad x \in [0,1] \end{displaymath}$

with $\mathbf{u} : [0,1] \to \mathbf{R}$ being sought for a given right hand side $\mathbf{f} : [0,1] \to \mathbf{R}$ , the Galerkin discretisation with constant ansatz functions 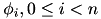$\phi_i, 0 \le i < n$

$\phi_i(x) = \left\{ \begin{array}{ll} 1, & x \in \left[\frac{i}{n},\frac{i+1}{n} \right] \\ 0, & \mathrm{otherwise} \end{array} \right.$

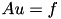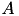leads to a linear equation system $A u = f$ where $u$ contains the coefficients of the discretised $\mathbf{u}$ and $A$ is defined by

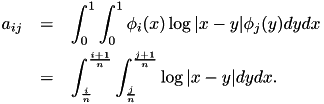
$\begin{eqnarray*} a_{ij} & = & \int_0^1 \int_0^1 \phi_i(x) \log|x-y| \phi_j(y) dy dx \\ & = & \int_{\frac{i}{n}}^{\frac{i+1}{n}} \int_{\frac{j}{n}}^{\frac{j+1}{n}} \log|x-y| dy dx \nonumber . \end{eqnarray*}$

The right hand side $f$ is given by

$f_i = \int_0^1 \phi_i(x) f(x) dx.$

Remarks: This example is identical to the introductory example in [BoerGraHac:2003b]}.

Coordinates and Cluster Trees

The code starts with the standard initialisation:

#include <hlib.hh>
using namespace HLIB;
  
int main ( int argc, char ** argv ) 
{
  try
  {
    INIT();
    CFG::set_verbosity( 3 );

Together with the initialisation, the verbosity level of HLIBpro was increased to have additional output during execution. The corresponding function set_verbosity is available in the namespace HLIB::CFG.

For clustering the unknowns, coordinate information is to be defined. For this 1d example, the indices are placed in the middle of equally sized intervals.

const size_t            n = 1024;
const double            h = 1.0 / double(n);
std::vector< double * > vertices( n );
for ( size_t i = 0; i < n; i++ )
{
    vertices[i]    = new double;
    vertices[i][0] = h * double(i) + ( h / 2.0 ); // center of [i/h,(i+1)/h]
}// for
autoptr< TCoordinate >  coord( new TCoordinate( vertices, 1 ) );

Coordinates in HLIBpro are vectors of the corresponding dimension, e.g. one in for this problem. The set of all coordinates is stored in objects of type TCoordinate.

The usage of autoptr (see ???) is advised, and extensively used in HLIBpro, since it decreases the possibility of memory leaks by automatically deleting the objects upon destruction of the autopointer variable, e.g. when leaving the local block.

Having coordinates for each index, the cluster tree and block cluster tree can be constructed.

TAutoBSPPartStrat             part_strat( coord.get() );
TBSPCTBuilder                 ct_builder( & part_strat, 20 );
autoptr< TClusterTree >       ct( ct_builder.build( coord.get() ) );

For the cluster tree, the partitioning strategy for the indices is determined automatically by TAutoBSPPartStrat. Furthermore, a $n_{\min}$ of size 20 is used during construction.

TStdAdmCond                   adm_cond( 2.0 );
TBCBuilder                    bct_builder;
autoptr< TBlockClusterTree >  bct( bct_builder.build( ct.get(), ct.get(),
                                   & adm_cond ) );

For the block cluster tree, the standard admissibility condition (see {eqn:std_adm}) implemented in TStdAdmCond is used with 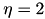$\eta = 2$ .

Matrix Construction and Coefficient Function

Using the block cluster tree, finally the 𝓗-matrix can be constructed. For this, adaptive cross approximation (ACA, see ???) is applied to compute low rank approximations of admissibly matrix blocks. In HLIBpro, an improved version of ACA is implemented in TACAPlus.

ACA only needs access to the matrix coefficients of the dense matrix. Those are provided by TLogCoeffFn, which will be discussed below. Finally, the block wise accuracy of the 𝓗-matrix approximation has to be defined using TTruncAcc objects. In this case, an accuracy of 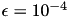$\epsilon = 10^{-4}$ is used.

TLogCoeffFn             coefffn( h, ct->perm_i2e(), ct->perm_i2e() );
TACAPlus< real >        aca( & coefffn );
TDenseMBuilder< real >  h_builder( & coefffn, & aca );
TTruncAcc               acc( 1e-4, 0.0 );
autoptr< TMatrix >      A;
A = h_builder.build( mach_info.nthreads(), bct.get(), acc );

Matrix construction is one example of a parallelised algorithm in HLIBpro. For shared memory systems only the number of threads are needed to define the degree of parallelism. Here, the maximal number of threads available for the program is used, which is stored in mach_info.

The coefficient function used during matrix construction is implemented in class TLogCoeffFn.

class TLogCoeffFn : public TPermCoeffFn< real > {

It is derived from TPermCoeffFn, where the interface is defined for coefficient evaluation with permuted indices. The reordering is necessary, since due to the construction of the cluster tree the numbering of the indices in the 𝓗-matrix is usually different from the corresponding numbering in the application. The latter is referred to as the external numbering, whereas the first is called the internal numbering.

Going on with TLogCoeffFn, the step width for the grid is stored as an internal variable for kernel evaluation:

private:

const double _h;

In the constructor, the permutation for mapping the internal to the external numbering are provided, both for rows and for columns, together with the step width:

public:
    TLogCoeffFn ( const double         h,
                  const TPermutation * row_perm,
                  const TPermutation * col_perm )
            : TPermCoeffFn< real >( row_perm, col_perm ),
              _h(h)
    {}

The actual interface for the evaluation of the matrix coefficients is implemented by the function eval, which is defined in TPermCoeffFn and has to be overloaded:

virtual void eval  ( const std::vector< idx_t > &  rowidxs,
                     const std::vector< idx_t > &  colidxs,
                     real *                        matrix ) const
{
      const size_t  n = rowidxs.size();
      const size_t  m = colidxs.size();
      for ( size_t  j = 0; j < m; ++j )
      {
          const int  idx1 = colidxs[ j ];
          
          for ( size_t  i = 0; i < n; ++i )
          {
              const int  idx0 = rowidxs[ i ];
              double     value;
              if ( idx0 == idx1 ) 
                  value = -1.5*_h*_h + _h*_h*std::log(_h);
              else
              {
                  const double dist = _h * ( std::abs( idx0 - idx1 ) - 1 );
                  const double t1   = dist+1.0*_h;
                  const double t2   = dist+2.0*_h;
          
                  value = ( - 1.5*_h*_h + 0.5*t2*t2*std::log(t2)
                            - t1*t1*std::log(t1) );
          
                  if ( std::abs(dist) > 1e-8 )
                      value += 0.5*dist*dist*std::log(dist);
              }// if
      
              matrix[ j*n + i ] = -value;
          }// for
      }// for
  }

This functions gets a set of indices for rows (rowidxs) and columns (colidxs) and a pointer to a memory block, where all the coefficients should be stored. The indices in both sets are already in the external numbering, hence the indices can directly be used for kernel evaluation. The mapping was performed by TPermCoeffFn. The memory layout of matrix is column wise, which holds for almost all data in HLIBpro. This is due to the memory layout of BLAS/LAPACK, originally implemented in Fortran, which uses column wise storage.

TPermCoeffFn is derived from TCoeffFn, which uses a slightly different evaluation interface based on index sets in the internal numbering. TPermCoeffFn overloads this method with the conversion between both numberings and implements the new eval method. To avoid compiler warnings about ``hidden functions'', the first version is brought into local scope by

using TPermCoeffFn< real >::eval;

By default, the format of the final matrix defined by the coefficients will be unsymmetric, e.g. lower and upper half of the matrix will be built. Please note, that this will not effect the actual algebraic matrix which may still be symmetric or hermtitian. Only the storage and subsequent algorithms are affected in terms of computational costs.

To change the matrix format, the function matrix_format has to be overloaded. In this case, as the matrix is symmetric, this looks like

virtual matform_t matrix_format () const { return MATFORM_SYM; }

Finally, TLogCoeffFn has to signal the value type, e.g. real or complex valued, to the matrix construction object with the method is_complex.

virtual bool is_complex () const { return false; }

};

It should be noted, that for a complex coefficient function, to evaluation method is not called eval but ceval.

𝓗-LU Factorisation

Having constructed the 𝓗-matrix, the corresponding equation system shall be solved. In most cases, a standard iterative solve will not be sufficient, e.g. either the convergence rate is to bad or there is no convergence at all. Therefore, a (good) preconditioner is needed, with the inverse of $A$ being the best possible. Since iterative schemes, only need matrix-vector multiplication, the corresponding functionality for the inverse is sufficient. This is provided by an (𝓗-) LU factorisation of $A$ , or for the symmetric case, a LDL factorisation:

autoptr< TMatrix >  B( A->copy() );
TLDL                ldl;
ldl.factorise( mach_info.nthreads(), B.get(), acc );

Since A is modified during the factorisation, a copy is constructed. The LDL factorisation is implemented in TLDL and makes use of multiple threads. The accuracy is chosen to be equal as during matrix construction.

B now contains the matrix data of the LDL factorisation, but computing the matrix-vector product is now no longer possible, since the special layout of the LDL data, e.g. diagonal and lower triangular part, is unknown to the matrix object itself. For this, an object of type TLDLInvMatrix has to be used, which allows the matrix-vector evaluation of the LDL factorisation stored in B. TLDLInvMatrix also has to know the format of 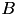$B$ , e.g. symmetric or hermitian.

TLDLInvMatrix A_inv( B.get(), MATFORM_SYM );

Iterative Solvers

Still missing is the right hand side of the equation system. In this example, it was chosen, such that 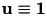$\mathbf{u} \equiv \mathbf{1}$ :

autoptr< TVector >  b( A->row_vector() );
for ( size_t  i = 0; i < n; i++ )
    b->set_entry( i, rhs( i, n ) );

with rhs defined by

real rhs ( const idx_t  i,
           const idx_t  n )
{
    const real  a     = real(i)           / real(n);
    const real  b     = (real(i)+real(1)) / real(n);
    real        value = -1.5 * (b - a);
  
    if ( std::abs( b )       > 1e-8 ) value += 0.5*b*b*std::log(b);
    if ( std::abs( a )       > 1e-8 ) value -= 0.5*a*a*std::log(a);
    if ( std::abs( 1.0 - b ) > 1e-8 ) value -= 0.5*(1.0-b)*(1.0-b)*
                                               std::log(1.0-b);
    if ( std::abs( 1.0 - a ) > 1e-8 ) value += 0.5*(1.0-a)*(1.0-a)*
                                               std::log(1.0-a); 
  
    return value;
}

For the iterative solver TAutoSolver is used, which automatically chooses a suitable solver for the given combination of matrix and preconditioner. Furthermore, statistics about the solution process is stored in an object of type TSolver::TInfo, e.g. convergence rate, number of steps.

TAutoSolver         solver( 1000 );
TSolver::TInfo      solve_info;
autoptr< TVector >  x;
x = A->col_vector();
solver.solve( A.get(), x.get(), b.get(), & A_inv, & solve_info );

To check the accuracy of the computed solution, we compare it with the known exact solution:

autoptr< TVector > sol( b->copy() );
sol->fill( 1.0 );
x->axpy( 1.0, sol.get() );
std::cout << "  |x-x~| = " << x->norm2() << std::endl;

The standard finalisation and catch block finishes the example:

    DONE();
  }// try
  catch ( Error & e )
  {
    std::cout << e.to_string() << std::endl;
  }// catch
  return 0;
}

The Plain Program

#include <hlib.hh>
using namespace HLIB;
  
class TLogCoeffFn : public TPermCoeffFn< real > {
private:
    const double  _h;
public:
    TLogCoeffFn ( const double         h,
                  const TPermutation * row_perm,
                  const TPermutation * col_perm )
            : TPermCoeffFn( row_perm, col_perm ),
              _h(h)
    {}
  virtual void eval  ( const std::vector< idx_t > &  rowidxs,
                       const std::vector< idx_t > &  colidxs,
                       real *                        matrix ) const
  {
        const size_t  n = rowidxs.size();
        const size_t  m = colidxs.size();
        for ( size_t  j = 0; j < m; ++j )
        {
            const int  idx1 = colidxs[ j ];
            
            for ( size_t  i = 0; i < n; ++i )
            {
                const int  idx0 = rowidxs[ i ];
                double     value;
                if ( idx0 == idx1 ) 
                    value = -1.5*_h*_h + _h*_h*std::log(_h);
                else
                {
                    const double dist = _h * ( std::abs( idx0 - idx1 ) - 1 );
                    const double t1   = dist+1.0*_h;
                    const double t2   = dist+2.0*_h;
            
                    value = ( - 1.5*_h*_h + 0.5*t2*t2*std::log(t2)
                              - t1*t1*std::log(t1) );
            
                    if ( std::abs(dist) > 1e-8 )
                        value += 0.5*dist*dist*std::log(dist);
                }// if
        
                matrix[ j*n + i ] = -value;
            }// for
        }// for
    }
    using TPermCoeffFn< real >::eval;
    virtual matform_t  matrix_format  () const { return MATFORM_SYM; }
    virtual bool       is_complex     () const { return false; }
};
real rhs ( const idx_t  i,
           const idx_t  n )
{
    const real  a     = real(i)           / real(n);
    const real  b     = (real(i)+real(1)) / real(n);
    real        value = -1.5 * (b - a);
  
    if ( std::abs( b )       > 1e-8 ) value += 0.5*b*b*std::log(b);
    if ( std::abs( a )       > 1e-8 ) value -= 0.5*a*a*std::log(a);
    if ( std::abs( 1.0 - b ) > 1e-8 ) value -= 0.5*(1.0-b)*(1.0-b)*
                                               std::log(1.0-b);
    if ( std::abs( 1.0 - a ) > 1e-8 ) value += 0.5*(1.0-a)*(1.0-a)*
                                               std::log(1.0-a); 
  
    return value;
}
int main ( int argc, char ** argv ) 
{
  try
  {
    INIT();
    CFG::set_verbosity( 3 );
    const size_t            n = 1024;
    const double            h = 1.0 / double(n);
    std::vector< double * > vertices( n );
    for ( size_t i = 0; i < n; i++ )
    {
        vertices[i]    = new double;
        vertices[i][0] = h * double(i) + ( h / 2.0 ); // center of [i/h,(i+1)/h]
    }// for
    autoptr< TCoordinate >  coord( new TCoordinate( vertices, 1 ) );
    TAutoBSPPartStrat             part_strat( coord.get() );
    TBSPCTBuilder                 ct_builder( & part_strat, 20 );
    autoptr< TClusterTree >       ct( ct_builder.build( coord.get() ) );
    TStdAdmCond                   adm_cond( 2.0 );
    TBCBuilder                    bct_builder;
    autoptr< TBlockClusterTree >  bct( bct_builder.build( ct.get(), ct.get(),
                                       & adm_cond ) );
    TLogCoeffFn             coefffn( h, ct->perm_i2e(), ct->perm_i2e() );
    TACAPlus< real >        aca( & coefffn );
    TDenseMBuilder< real >  h_builder( & coefffn, & aca );
    TTruncAcc               acc( 1e-4, 0.0 );
    autoptr< TMatrix >      A;
    A = h_builder.build( mach_info.nthreads(), bct.get(), acc );
    autoptr< TMatrix >   B( A->copy() );
    TLDL                 ldl;
    
    ldl.factorise( mach_info.nthreads(), B.get(), acc );
    TLDLInvMatrix  A_inv( B.get(), MATFORM_SYM );
    autoptr< TVector >   b( A->row_vector() );
    for ( size_t  i = 0; i < n; i++ )
        b->set_entry( i, rhs( i, n ) );
    TAutoSolver          solver( 1000 );
    TSolver::TInfo       solve_info;
    autoptr< TVector >   x;
    x = A->col_vector();
    solver.solve( A.get(), x.get(), b.get(), & A_inv, & solve_info );
    autoptr< TVector > sol( b->copy() );
    sol->fill( 1.0 );
    x->axpy( 1.0, sol.get() );
    
    std::cout << "  |x-x~| = " << x->norm2() << std::endl;
    DONE();
  }// try
  catch ( Error & e )
  {
    std::cout << e.to_string() << std::endl;
  }// catch
  return 0;
}