Table of contents

In this example, an integral equation is to be solved by representing the discretised operator with an 𝓗-matrix, whereby the 𝓗-matrix is constructed using a matrix coefficient function for entries of the equation system. Furthermore, for the iterative solver a preconditioner is computed using 𝓗-LU factorisation.

Problem Description

Given the integral equation

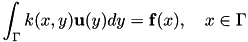
$\begin{displaymath} \int_{\Gamma} k(x,y) \mathbf{u}(y) dy = \mathbf{f}(x), \quad x \in \Gamma \end{displaymath}$

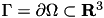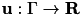with $\Gamma = \partial \Omega \subset \mathbf{R}^3$ and $\mathbf{u} : \Gamma \to \mathbf{R}$ being sought for a given right hand side 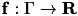$\mathbf{f} : \Gamma \to \mathbf{R}$ , the Galerkin discretisation with ansatz functions 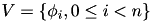$V = \{\phi_i, 0 \le i < n\}$ and test functions 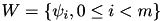$W = \{\psi_i, 0 \le i < m\}$ leads to a linear equation system

$A u = f$

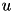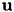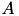where $u$ contains the coefficients of the discretised $\mathbf{u}$ and $A$ is defined by

$a_{ij} = \int_\Gamma \int_\Gamma \phi_i(x) k(x,y) \psi_j(y) dy dx$

The right hand side 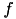$f$ is given by

$f_i = \int_{\Gamma} \psi_i(x) f(x) dx.$

Surface Grid and Function Spaces

The code starts with the standard initialisation:

#include <hlib.hh>
using namespace HLIB;
  
int main ( int argc, char ** argv ) 
{
  try
  {
    INIT();

𝓗𝖫𝖨𝖡𝗉𝗋𝗈 supports triangular surface grids and can load such grids stored in several file formats, e.g. HLIB, PLY, SurfaceMesh and Gmsh v2 format. Although individual I/O classes for each file format exist, you may also use automatic file format detection:

autoptr< TGrid > grid = load_grid( "grid.tri" );

Based upon the grid, function spaces for the ansatz and the test space are defined. For Laplace and Helmholtz kernels, piecewise constant and linear function spaces are available, whereas for Maxwell kernels, piecewise constant edge space (RWG elements) is implemented.

autoptr< TLinearFnSpace > ansatz_fnspace( new ansatzsp_t( grid.get() ) );

autoptr< TLinearFnSpace > test_fnspace( new testsp_t( grid.get() ) );

Remarks: Different grids may be used for ansatz and test spaces.

The functions spaces provide necessary geometrical information for construction cluster trees and block cluster trees for the defined index sets:

autoptr< TCoordinate >   coord1( ansatz_fnspace->build_coord() );
autoptr< TCoordinate >   coord2( test_fnspace->build_coord() );
autoptr< TClusterTree >  ct1, ct2;
{ 
    TAutoBSPPartStrat    part_strat( coord1.get() );
    TBSPCTBuilder        ct_builder( & part_strat );
  
    ct1 = ct_builder.build( coord1.get() );
}
{ 
    TAutoBSPPartStrat    part_strat( coord2.get() );
    TBSPCTBuilder        ct_builder( & part_strat );
  
    ct2 = ct_builder.build( coord2.get() );
}
TStdAdmCond                   adm_cond;
TBCBuilder                    bct_builder;
autoptr< TBlockClusterTree >  bct( bct_builder.build( ct1.get(), ct2.get(), & adm_cond ) );

Definition of Kernel Function and Matrix Construction

In 𝓗𝖫𝖨𝖡𝗉𝗋𝗈, different kernels are defined by special bilinear forms, each derived from TBEMBF. For reasons of efficiency, e.g. for basis function evaluation, the ansatz spaces are provided to each bilinear form as template arguments. For the Helmholtz single layer potential, the corresponding bilinear form is declared as:

typedef  THelmholtzSLPBF< ansatzsp_t, testsp_t >  slpbf_t;
complex  kappa( -2, 1 );
slpbf_t  slpbf( kappa, ansatz_fnspace.get(), test_fnspace.get() );

Here, kappa is the wave number of the underlying problem.

Remarks: When template based classes are used, as here with the Helmholtz bilinear form, type aliases will increase readability of the code.

For matrix construction, the bilinear form is not fully sufficient as actual matrix coefficients are needed. These are provided by a special coefficient function:

TBFCoeffFn< slpbf_t > coeff_fn( & slpbf, bct->row_ct()->perm_i2e(), bct->col_ct()->perm_i2e() );

Finally, the low-rank approximation technique and the block-wise accuracy gave to be defined, being ACA+ and 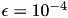$\epsilon = 10^{-4}$ in our case. Equipped with these, the TDenseMBuilder class can construct the discretised Helmholtz single layer potential:

TACAPlus< complex >        aca( & coeff_fn );
TTruncAcc                  acc( eps, 0.0 );
TDenseMBuilder< complex >  h_builder( & coeff_fn, & aca );
autoptr< TMatrix >         A;
A = h_builder.build( mach_info.nthreads(), bct.get(), acc );

Since matrix construction is available in thread parallel form, you may choose to use more than one processor (or thread) for build the 𝓗-matrix. In mach_info necessary information about the current maximal number of threads are stored.

Building the Right-hand Side

Building the right-hand side 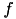$f$ is again performed using quadrature rules over the triangular grid. The corresponding class implementing the quadrature formula is TQuadBEMRHS.

TMyRHS                            rhsfn;
TQuadBEMRHS< testsp_t, complex >  rhs_build( 4 );
autoptr< TVector >                rhs( rhs_build.build( ct2->root(),
                                                        test_fnspace.get(),
                                                        & rhsfn,
                                                        ct2->perm_i2e() ) );

The function 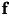$\mathbf{f}$ is hereby provided in the form of a TBEMFunction, or, to be precise a derived class where the method eval has to be overloaded:

class TMyRHS : public TBEMFunction< complex >
{
public:
    virtual complex
    eval ( const T3Point &  pos,
           const T3Point &  ) const
    {
        return std::sin( pos.x() ) * std::cos( pos.y() );
    }
};

In both cases, the quadrature formula and the BEM function, the value type complex and the function space (for TQuadBEMRHS) are defined as template arguments.

Solving the Discretised System

As standard iteration schemes will usually fail with the above equation system, 𝓗-LU preconditioning is used to ensure and to speed up convergence.

autoptr< TMatrix > B( A->copy() );

autoptr< TMatrix > A_inv( factorise_inv( mach_info.nthreads(), B.get(), acc ); )

Since the matrix is modified during LU factorisation, a copy of it has to be created and provided for factorisation. The result of factorise_inv is a matrix object suitable for evaluation of the inverse of 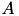$A$ and can be used for preconditioning:

TSolver::TInfo      solve_info;
autoptr< TVector >  x;
x = A->col_vector();
solve( A.get(), x.get(), b.get(), & A_inv, & solve_info );

Upon exit, x contains the computed solution to the initial discrete problem.

The standard finalisation and catch block finishes the example:

    DONE();
  }// try
  catch ( Error & e )
  {
    std::cout << e.to_string() << std::endl;
  }// catch
  return 0;
}

The Plain Program

#include <hlib.hh>
using namespace HLIB;
  
class TMyRHS : public TBEMFunction< complex >
{
public:
    virtual complex
    eval ( const T3Point &  pos,
           const T3Point &  ) const
    {
        return std::sin( pos.x() ) * std::cos( pos.y() );
    }
};
int main ( int argc, char ** argv ) 
{
  try
  {
    INIT();
    autoptr< TGrid >                  grid = load_grid( "grid.tri" );
    autoptr< TLinearFnSpace >         ansatz_fnspace( new TLinearFnSpace( grid.get() ) );
    autoptr< TLinearFnSpace >         test_fnspace(   new TLinearFnSpace( grid.get() ) );
    autoptr< TCoordinate >            coord1( ansatz_fnspace->build_coord() );
    autoptr< TCoordinate >            coord2( test_fnspace->build_coord() );
    autoptr< TClusterTree >           ct1, ct2;
    { 
        TAutoBSPPartStrat             part_strat( coord1.get() );
        TBSPCTBuilder                 ct_builder( & part_strat );
      
        ct1 = ct_builder.build( coord1.get() );
    }
    { 
        TAutoBSPPartStrat             part_strat( coord2.get() );
        TBSPCTBuilder                 ct_builder( & part_strat );
      
        ct2 = ct_builder.build( coord2.get() );
    }
    TStdAdmCond                       adm_cond;
    TBCBuilder                        bct_builder;
    autoptr< TBlockClusterTree >      bct( bct_builder.build( ct1.get(), ct2.get(), & adm_cond ) );
    typedef  THelmholtzSLPBF< TLinearFnSpace, TLinearFnSpace >  slpbf_t;
    complex                           kappa( -2, 1 );
    slpbf_t                           slpbf( kappa, ansatz_fnspace.get(), test_fnspace.get() );
    TBFCoeffFn< slpbf_t >             coeff_fn( & slpbf, bct->row_ct()->perm_i2e(), bct->col_ct()->perm_i2e() );
    TACAPlus< complex >               aca( & coeff_fn );
    TTruncAcc                         acc( eps, 0.0 );
    TDenseMBuilder< complex >         h_builder( & coeff_fn, & aca );
    autoptr< TMatrix >                A;
    A = h_builder.build( mach_info.nthreads(), bct.get(), acc );
    TMyRHS                            rhsfn;
    TQuadBEMRHS< TLinearFnSpace, complex >  
                                      rhs_build( 4 );
    autoptr< TVector >                rhs( rhs_build.build( ct2->root(),
                                                            test_fnspace.get(),
                                                            & rhsfn,
                                                            ct2->perm_i2e() ) );
    autoptr< TMatrix >                B( A->copy() );
    autoptr< TMatrix >                A_inv( factorise_inv( mach_info.nthreads(), B.get(), acc ); )
    TSolver::TInfo                    solve_info;
    autoptr< TVector >                x( A->col_vector() );
    solve( A.get(), x.get(), b.get(), & A_inv, & solve_info );
    DONE();
  }// try
  catch ( Error & e )
  {
    std::cout << e.to_string() << std::endl;
  }// catch
  return 0;
}