implements Jacobi preconditioner More...

#include <TJacobi.hh>

Inheritance diagram for TJacobi:

Public Member Functions
	TJacobi (TMatrix *A, const real damping=1.0)

const TMatrix *	matrix () const
	return sparse matrix

real	damping_factor () const
	return damping factor

bool	is_complex () const
	return true, if field type is complex

bool	is_self_adjoint () const
	return true, of operator is self adjoint

virtual void	apply (const TVector x, TVector y, const matop_t op) const

virtual void	apply_add (const real alpha, const TVector x, TVector y, const matop_t op) const

virtual auto	domain_vector () const -> std::unique_ptr< TVector >
	return vector in domain space

virtual auto	range_vector () const -> std::unique_ptr< TVector >
	return vector in range space

Public Member Functions inherited from TTypeInfo
virtual typeid_t	type () const =0
	return type ID of object

virtual bool	is_type (const typeid_t t) const
	return true if local object is of given type ID t

virtual std::string	typestr () const
	return string representation of type

Detailed Description

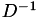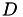TJacobi provides application of a Jacobi type preconditioner for a given matrix A, e.g. $D^{-1}$ with $D$ being the diagonal of A. Here, A may be of any type, e.g. dense, low-rank, block or sparse matrix. The diagonal elements are assumed to be non-zero.

Constructor & Destructor Documentation

TJacobi	(	TMatrix *	A,
		const real	damping = `1.0`
	)

construct Jacobi preconditioner based on sparse matrix A with damping factor damping

Member Function Documentation

virtual void apply	(	const TVector *	x,
		TVector *	y,
		const matop_t	op
	)		const

virtual

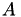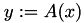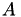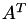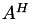mapping function of linear operator $A$ , e.g. $ y := A(x)$ . Depending on op, either $A$ , $A^T$ or $A^H$ is applied.

Implements TLinearOperator.

virtual void apply_add	(	const real	alpha,
		const TVector *	x,
		TVector *	y,
		const matop_t	op
	)		const

virtual

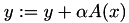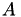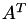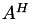mapping function with update: $y := y + \alpha A(x)$ . Depending on op, either $A$ , $A^T$ or $A^H$ is applied.

Implements TLinearOperator.

Public Member Functions

Detailed Description

Constructor & Destructor Documentation

Member Function Documentation