|
|
template<typename T1 , typename T2 > |
| enable_if< is_vector< T2 >::value &&is_same_type< T1, typename T2::value_t >::value >::result | fill (const T1 f, T2 &x) |
| | fill vector with constant
|
| |
|
template<typename T1 > |
| enable_if< is_vector< T1 >::value >::result | conj (T1 &x) |
| | conjugate entries in vector
|
| |
|
template<typename T1 , typename T2 > |
| enable_if< is_vector< T2 >::value &&is_same_type< T1, typename T2::value_t >::value >::result | scale (const T1 f, T2 &x) |
| | scale vector by constant
|
| |
|
template<typename T1 , typename T2 > |
| enable_if< is_vector< T1 >::value &&is_vector< T2 >::value &&is_same_type< typename T1::value_t, typename T2::value_t >::value >::result | copy (const T1 &x, T2 &y) |
| | copy x into y
|
| |
|
template<typename T1 , typename T2 > |
| enable_if< is_vector< T1 >::value &&is_vector< T2 >::value &&is_same_type< typename T1::value_t, typename T2::value_t >::value >::result | swap (T1 &x, T2 &y) |
| | exchange x and y
|
| |
|
template<typename T1 > |
| enable_if_res< is_vector< T1 >::value, idx_t >::result | max_idx (const T1 &x) |
| | determine index with maximal absolute value in x
|
| |
|
template<typename T1 > |
| enable_if_res< is_vector< T1 >::value, idx_t >::result | min_idx (const T1 &x) |
| | determine index with minimax absolute value in x
|
| |
|
template<typename T1 , typename T2 , typename T3 > |
| enable_if< is_vector< T2 >::value &&is_vector< T3 >::value &&is_same_type< T1, typename T2::value_t >::value &&is_same_type< T1, typename T3::value_t >::value >::result | add (const T1 alpha, const T2 &x, T3 &y) |
| | compute y ≔ y + α·x
|
| |
|
template<typename T1 , typename T2 > |
| enable_if_res< is_vector< T1 >::value &&is_vector< T2 >::value &&is_same_type< typename T1::value_t, typename T2::value_t >::value, typename T1::value_t >::result | dot (const T1 &x, const T2 &y) |
| | compute <x,y> = x^H · y
|
| |
|
template<typename T1 , typename T2 > |
| enable_if_res< is_vector< T1 >::value &&is_vector< T2 >::value &&is_same_type< typename T1::value_t, typename T2::value_t >::value, typename T1::value_t >::result | dotu (const T1 &x, const T2 &y) |
| | compute <x,y> without conjugating x, e.g. x^T · y
|
| |
| template<typename T1 > |
| enable_if_res< is_vector< T1 >::value, typename real_type< typename T1::value_t >::type_t >::result | norm2 (const T1 &x) |
| | compute ∥x∥₂ More...
|
| |
|
template<typename T1 > |
| bool | abs_lt (const T1 a1, const T1 a2) |
| |
| template<typename T1 , typename T2 > |
| enable_if_res< is_vector< T1 >::value &&is_vector< T2 >::value &&is_same_type< typename T1::value_t, typename T2::value_t >::value, typename T1::value_t >::result | stable_dotu (const T1 &x, const T2 &y) |
| | compute dot product x · y numerically stable More...
|
| |
| template<typename T1 > |
| enable_if_res< is_vector< T1 >::value, typename T1::value_t >::result | stable_sum (const T1 &x) |
| | compute sum of elements in x numerically stable More...
|
| |
|
|
template<typename T1 > |
| enable_if< is_matrix< T1 >::value >::result | transpose (T1 &A) |
| | transpose matrix A: A → A^T ASSUMPTION: A is square matrix
|
| |
|
template<typename T1 > |
| enable_if< is_matrix< T1 >::value >::result | conj_transpose (T1 &A) |
| | conjugate transpose matrix A: A → A^H ASSUMPTION: A is square matrix
|
| |
|
template<typename T1 > |
| enable_if< is_matrix< T1 >::value >::result | max_idx (const T1 &M, idx_t &row, idx_t &col) |
| | determine index (i,j) with maximal absolute value in M and return in row and col
|
| |
|
template<typename T1 , typename T2 , typename T3 , typename T4 > |
| enable_if< is_vector< T2 >::value &&is_vector< T3 >::value &&is_matrix< T4 >::value &&is_same_type< T1, typename T2::value_t >::value &&is_same_type< T1, typename T3::value_t >::value &&is_same_type< T1, typename T4::value_t >::value >::result | add_r1 (const T1 alpha, const T2 &x, const T3 &y, T4 &A) |
| | compute A ≔ A + α·x·y^H
|
| |
|
template<typename T1 , typename T2 , typename T3 , typename T4 > |
| enable_if< is_vector< T2 >::value &&is_vector< T3 >::value &&is_matrix< T4 >::value &&is_same_type< T1, typename T2::value_t >::value &&is_same_type< T1, typename T3::value_t >::value &&is_same_type< T1, typename T4::value_t >::value >::result | add_r1u (const T1 alpha, const T2 &x, const T3 &y, T4 &A) |
| | compute A ≔ A + α·x·y^T
|
| |
|
template<typename T1 , typename T2 , typename T3 , typename T4 > |
| enable_if< is_matrix< T2 >::value &&is_vector< T3 >::value &&is_vector< T4 >::value &&is_same_type< T1, typename T2::value_t >::value &&is_same_type< T1, typename T3::value_t >::value &&is_same_type< T1, typename T4::value_t >::value >::result | mulvec (const T1 alpha, const T2 &A, const T3 &x, const T1 beta, T4 &y) |
| | compute y ≔ β·y + α·A·x
|
| |
|
template<typename T1 , typename T2 > |
| enable_if< is_matrix< T1 >::value &&is_vector< T2 >::value &&is_same_type< typename T1::value_t, typename T2::value_t >::value >::result | mulvec_tri (const tri_type_t shape, const diag_type_t diag, const T1 &A, T2 &x) |
| | compute x ≔ M·x, where M is upper or lower triangular with unit or non-unit diagonal
|
| |
|
template<typename T1 , typename T2 > |
| enable_if< is_matrix< T1 >::value &&is_vector< T2 >::value &&is_same_type< typename T1::value_t, typename T2::value_t >::value >::result | solve (T1 &A, T2 &b) |
| | solve A·x = b with known A and b; x overwrites b (A is overwritten upon exit!)
|
| |
|
template<typename T1 , typename T2 , typename T3 , typename T4 > |
| enable_if< is_matrix< T2 >::value &&is_matrix< T3 >::value &&is_matrix< T4 >::value &&is_same_type< T1, typename T2::value_t >::value &&is_same_type< T1, typename T3::value_t >::value &&is_same_type< T1, typename T4::value_t >::value >::result | prod (const T1 alpha, const T2 &A, const T3 &B, const T1 beta, T4 &C) |
| | compute C ≔ β·C + α·A·B
|
| |
|
template<typename T1 , typename T2 , typename T3 > |
| enable_if_res< is_matrix< T2 >::value &&is_matrix< T3 >::value &&is_same_type< T1, typename T2::value_t >::value &&is_same_type< T1, typename T3::value_t >::value, Matrix< typename T2::value_t > >::result | prod (const T1 alpha, const T2 &A, const T3 &B) |
| | compute C ≔ α·A·B
|
| |
|
template<typename T1 , typename T2 > |
| enable_if< is_matrix< T1 >::value &&is_matrix< T2 >::value &&is_same_type< typename T1::value_t, typename T2::value_t >::value >::result | hadamard_prod (const T1 &A, T2 &B) |
| | compute B ≔ A⊙B, e.g. Hadamard product
|
| |
|
template<typename T1 , typename T2 , typename T3 > |
| enable_if< is_matrix< T2 >::value &&is_matrix< T3 >::value &&is_same_type< T1, typename T2::value_t >::value &&is_same_type< T1, typename T3::value_t >::value >::result | prod_tri (const eval_side_t side, const tri_type_t uplo, const diag_type_t diag, const T1 alpha, const T2 &A, T3 &B) |
| | compute B ≔ α·A·B or B ≔ α·B·A with triangular matrices
|
| |
|
template<typename T1 , typename T2 > |
| enable_if< is_matrix< T1 >::value &&is_vector< T2 >::value &&is_same_type< typename real_type< typename T1::value_t >::type_t, typename real_type< typename T2::value_t >::type_t >::value >::result | prod_diag (T1 &M, const T2 &D, const idx_t k) |
| | multiply k columns of M with diagonal matrix D, e.g. compute M ≔ M·D
|
| |
|
template<typename T1 > |
| enable_if_res< is_matrix< T1 >::value, typename real_type< typename T1::value_t >::type_t >::result | normF (const T1 &M) |
| | return Frobenius norm of M
|
| |
|
template<typename T1 , typename T2 > |
| enable_if_res< is_matrix< T1 >::value &&is_matrix< T2 >::value &&is_same_type< typename T1::value_t, typename T2::value_t >::value, typename real_type< typename T1::value_t >::type_t >::result | normF (const T1 &A, const T2 &B) |
| | compute Frobenius norm of A-B
|
| |
| template<typename T1 > |
| enable_if_res< is_matrix< T1 >::value, typename real_type< typename T1::value_t >::type_t >::result | cond (const T1 &M) |
| | return condition of M More...
|
| |
|
template<typename T1 > |
| enable_if< is_matrix< T1 >::value >::result | make_symmetric (T1 &A) |
| | make given matrix symmetric, e.g. copy lower left part to upper right part
|
| |
|
template<typename T1 > |
| enable_if< is_matrix< T1 >::value >::result | make_hermitian (T1 &A) |
| | make given matrix hermitian, e.g. copy conjugated lower left part to upper right part and make diagonal real
|
| |
|
|
template<typename T1 , typename T2 > |
| enable_if< is_matrix< T1 >::value &&is_vector< T2 >::value &&is_same_type< typename T1::value_t, typename T2::value_t >::value >::result | solve_tri (const tri_type_t uplo, const diag_type_t diag, const T1 &A, T2 &b) |
| | solve A·x = b with known A and b; x overwrites b
|
| |
|
template<typename T1 , typename T2 , typename T3 > |
| enable_if< is_matrix< T2 >::value &&is_matrix< T3 >::value &&is_same_type< T1, typename T2::value_t >::value &&is_same_type< T1, typename T3::value_t >::value >::result | solve_tri (const eval_side_t side, const tri_type_t uplo, const diag_type_t diag, const T1 alpha, const T2 &A, T3 &B) |
| | solve A·X = α·B or X·A· = α·B with known A and B; X overwrites B
|
| |
|
template<typename T1 > |
| enable_if< is_matrix< T1 >::value >::result | invert (T1 &A) |
| | invert matrix A; A will be overwritten with A^-1 upon exit
|
| |
|
template<typename T1 > |
| enable_if< is_matrix< T1 >::value >::result | invert (T1 &A, const tri_type_t tri_type, const diag_type_t diag_type) |
| | invert lower or upper triangular matrix A with unit or non-unit diagonal; A will be overwritten with A^-1 upon exit
|
| |
| template<typename T > |
| void | pseudo_invert (Matrix< T > &A, const TTruncAcc &acc) |
| | compute pseudo inverse of matrix A with precision acc More...
|
| |
|
template<typename T1 > |
| enable_if< is_matrix< T1 >::value >::result | lu (T1 &A) |
| | compute LU factorisation of the n×m matrix A with n×min(n,m) unit diagonal lower triangular matrix L and min(n,m)xm upper triangular matrix U; A will be overwritten with L and U upon exit
|
| |
|
template<typename T1 > |
| enable_if< is_matrix< T1 >::value >::result | llt (T1 &A) |
| | compute L·L^T factorisation of given symmetric n×n matrix A
|
| |
|
template<typename T1 > |
| enable_if< is_matrix< T1 >::value >::result | llh (T1 &A) |
| | compute L·L^H factorisation of given hermitian n×n matrix A
|
| |
|
template<typename T1 > |
| enable_if< is_matrix< T1 >::value >::result | ldlt (T1 &A) |
| | compute L·D·L^T factorisation of given symmetric n×n matrix A
|
| |
|
template<typename T1 > |
| enable_if< is_matrix< T1 >::value >::result | ldlh (T1 &A) |
| | compute L·D·L^H factorisation of given hermitian n×n matrix A
|
| |
|
template<typename T1 > |
| enable_if< is_matrix< T1 >::value >::result | qr (T1 &A, Matrix< typename T1::value_t > &R) |
| | compute QR factorisation of the n×m matrix A with n×m matrix Q and mxm matrix R (n >= m); A will be overwritten with Q upon exit
|
| |
|
template<typename T1 > |
| enable_if< is_matrix< T1 >::value >::result | eigen (T1 &M, Vector< typename T1::value_t > &eig_val, Matrix< typename T1::value_t > &eig_vec) |
| | compute eigenvalues and eigenvectors of matrix M
|
| |
| template<typename T1 > |
| enable_if< is_matrix< T1 >::value >::result | eigen (T1 &M, const Range &eig_range, Vector< typename T1::value_t > &eig_val, Matrix< typename T1::value_t > &eig_vec) |
| | compute selected (by eig_range) eigenvalues and eigenvectors of the symmetric matrix M More...
|
| |
|
template<typename T1 , typename T2 > |
| enable_if< is_vector< T1 >::value &&is_vector< T2 >::value &&is_same_type< typename T1::value_t, typename T2::value_t >::value >::result | eigen (T1 &diag, T2 &subdiag, Vector< typename T1::value_t > &eig_val, Matrix< typename T1::value_t > &eig_vec) |
| | compute eigenvalues and eigenvectors of the symmetric, tridiagonal matrix defines by diagonal coefficients in diag and off-diagonal coefficients subdiag
|
| |
|
template<typename T1 > |
| enable_if< is_matrix< T1 >::value >::result | svd (T1 &A, Vector< typename real_type< typename T1::value_t >::type_t > &S, Matrix< typename T1::value_t > &V) |
| | compute SVD decomposition 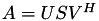 of the nxm matrix A with n×min(n,m) matrix U, min(n,m)×min(n,m) matrix S (diagonal) and m×min(n,m) matrix V; A will be overwritten with U upon exit of the nxm matrix A with n×min(n,m) matrix U, min(n,m)×min(n,m) matrix S (diagonal) and m×min(n,m) matrix V; A will be overwritten with U upon exit
|
| |
|
template<typename T1 > |
| enable_if< is_matrix< T1 >::value >::result | svd (T1 &A, Vector< typename real_type< typename T1::value_t >::type_t > &S, const bool left=true) |
| | compute SVD decomposition 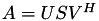 of the nxm matrix A but return only the left/right singular vectors and the singular values S ∈ ℝ^min(n,m); upon exit, A will be contain the corresponding sing. vectors of the nxm matrix A but return only the left/right singular vectors and the singular values S ∈ ℝ^min(n,m); upon exit, A will be contain the corresponding sing. vectors
|
| |
|
template<typename T1 > |
| enable_if< is_matrix< T1 >::value >::result | sv (T1 &A, Vector< typename real_type< typename T1::value_t >::type_t > &S) |
| | compute SVD decomposition 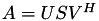 of the nxm matrix A but return only the singular values S ∈ ℝ^min(n,m); A will be overwritten with U upon exit of the nxm matrix A but return only the singular values S ∈ ℝ^min(n,m); A will be overwritten with U upon exit
|
| |
|
template<typename T1 , typename T2 > |
| enable_if< is_matrix< T1 >::value &&is_matrix< T2 >::value &&is_same_type< typename T1::value_t, typename T2::value_t >::value >::result | sv (T1 &A, T2 &B, Vector< typename real_type< typename T1::value_t >::type_t > &S) |
| | compute SVD decomposition 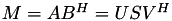 of the nxm low-rank matrix M but return only the singular values S ∈ ℝ^min(n,m); A and B will be overwritten upon exit of the nxm low-rank matrix M but return only the singular values S ∈ ℝ^min(n,m); A and B will be overwritten upon exit
|
| |
|
template<typename T1 > |
| enable_if_res< is_matrix< T1 >::value, size_t >::result | approx (T1 &M, const TTruncAcc &acc, Matrix< typename T1::value_t > &A, Matrix< typename T1::value_t > &B) |
| | approximate given dense matrix M by low rank matrix according to accuracy acc. The low rank matrix will be stored in A and B
|
| |
|
template<typename T > |
| size_t | truncate (Matrix< T > &A, Matrix< T > &B, const TTruncAcc &acc) |
| | truncate given A · B^H low rank matrix matrix (A being n×k and B being m×k) with respect to given accuracy acc; store truncated matrix in A(:,0:k-1) and B(:,0:k-1) where k is the returned new rank after truncation
|
| |
| template<typename T1 > |
| enable_if< is_matrix< T1 >::value >::result | factorise_ortho (T1 &A, Matrix< typename T1::value_t > &R) |
| | construct factorisation A = Q·R of A, with orthonormal Q More...
|
| |
| template<typename T > |
| void | factorise_ortho (Matrix< T > &A, Matrix< T > &R, const TTruncAcc &acc) |
| | construct approximate factorisation A = Q·R of A, with orthonormal Q More...
|
| |
This modules provides most low level algebra functions, e.g. vector dot products, matrix multiplication, factorisation and singular value decomposition. See also BLAS/LAPACK Interface for an introduction.
to your source files.
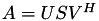 of the nxm matrix A with n×min(n,m) matrix U, min(n,m)×min(n,m) matrix S (diagonal) and m×min(n,m) matrix V; A will be overwritten with U upon exit
of the nxm matrix A with n×min(n,m) matrix U, min(n,m)×min(n,m) matrix S (diagonal) and m×min(n,m) matrix V; A will be overwritten with U upon exit 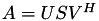 of the nxm matrix A but return only the left/right singular vectors and the singular values S ∈ ℝ^min(n,m); upon exit, A will be contain the corresponding sing. vectors
of the nxm matrix A but return only the left/right singular vectors and the singular values S ∈ ℝ^min(n,m); upon exit, A will be contain the corresponding sing. vectors 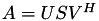 of the nxm matrix A but return only the singular values S ∈ ℝ^min(n,m); A will be overwritten with U upon exit
of the nxm matrix A but return only the singular values S ∈ ℝ^min(n,m); A will be overwritten with U upon exit 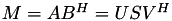 of the nxm low-rank matrix M but return only the singular values S ∈ ℝ^min(n,m); A and B will be overwritten upon exit
of the nxm low-rank matrix M but return only the singular values S ∈ ℝ^min(n,m); A and B will be overwritten upon exit 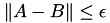 with
with 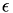 defined by acc.
defined by acc.  1.8.9.1
1.8.9.1