Table of Contents

Geometrical clustering uses geometrical information for each index, e.g. their spatial position, for grouping them. The standard algorithm uses some form of binary space partitioning, e.g. a splitting axis is chosen and the index set is halved with respect to this axis.

Coordinates

Before starting with the clustering itself, the coordinate information has to be provided to HLIBpro. For that, the class TCoordinate is available. Coordinates themself are stored as arrays with pointers to double arrays of the corresponding dimension. An example for equidistant indices with step width 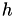$h$ in the 2D unit cube is:

const double             h = 0.1;
const size_t             n = ( 1.0 / h );
std::vector< double * >  coord_vec( n*n );
for ( int  y = 0; y <= n; ++y ) {
  for ( int  x = 0; x <= n; ++x ) {
      double *  c = new double[ 2 ];  // 2D
      c[0] = x*h;                     // X 
      c[1] = y*h;                     // Y
      coord_vec[ y*n + x ] = c;       // store column wise
  }   
}

Remarks: Please note, that the order, in which the coordinates are stored in coord does not matter as the indicies corresponding to these coordinates will be reordered due to clustering.

Once the data for the coordinates is available, the TCoordinate object can be created:

TCoordinate * coord = new TCoordinate( coord_vec, 2 );

A copy of the actual coordinate data will be created during construction. To prevent this and hence, to use the provided data, an optional flag may be given while calling the constructor:

TCoordinate * coord = new TCoordinate( coord_vec, 2, true );

In this case, coord will always reference data in coord_vec. Therefore, changing this data will also change the geometrical data in coord.

Typically, indices correspond to basis function steming from some form of discritisation and often have a small support. The size or extend of this support can used to further describe the actual index during construction, delivering more accurate cluster trees.

The support for each basis function may therefore also be stored in TCoordinate objects. Due to the different shape of such support, an approximation is assumed using a bounding box. This bounding box is defined for each index by its minimal and maximal coordinate:

std::vector< double * >  bbmin( n*n );
std::vector< double * >  bbmax( n*n );
for ( int  y = 0; y <= n; ++y ) {
  for ( int  x = 0; x <= n; ++x ) {
      double *  bmin = new double[ 2 ];
      double *  bmax = new double[ 2 ];
      bmin[0] = x*h - h; bmin[1] = y*h - h;
      bmax[0] = x*h + h; bmax[1] = y*h + h;
      bbmin[ y*n + x ] = bmin;
      bbmax[ y*n + x ] = bmax;
  }   
}
TCoordinate *  coord = new TCoordinate( coord_vec, 2, bbmin, bbmax );

Here, a bounding box of size $[-h,h]^2$ around each index coordinate is assumed.

Often, the geometry has some kind of periodicity, e.g. along one or all axis. This can also be defined in TCoordinate objects.

TPoint  period( 1, 0 );
coord->set_period( period );

Here, a periodicity with respect to the 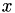$x$ axis was defined, such that the geometry repeats with a step width of 1.

Remarks: The periodicity only has influence on the clustering. If the problem to solve also contains some periodicity, this has to be explicitly modelled, e.g. during matrix construction.

Partitioning Strategy

After having defined all necessary geometrical information, the next step is choosing the right partitioning strategy for clustering. HLIBpro implements several such methods:

geometrically balanced: choose splitting axis such that all son clusters have equal volume (TGeomBSPPartStrat),
cardinality balanced: choose splitting axis such that all son clusters have the same number of indices (TCardBSPPartStrat),
principle component analysis (PCA): choose splitting axis by performing PCA of the coordinate set (TPCABSPPartStrat).

For the first two strategies, the technique can be altered such that all axis are chosen regularly (or cyclically), e.g. 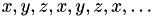$x,y,z,x,y,z,x,\ldots$ , which is needed for some low rank approximation algorithms, e.g. hybrid cross approximation.

Furthermore, an automatic strategy is available in which the coordinate data is analysed and a suitable partitioning strategy is chosen (TAutoBSPPartStrat), which defaults to geometrical clustering except in severly unbalanced cases.

TAutoBSPPartStrat part_strat( coord.get() );

Cluster Tree Constructor

Using the partitioning strategy, the actual constructing algorithm for the cluster tree can be started. Here, the following algorithms are available for geometrical clustering:

TBSPCTBuilder: standard binary space partitioning,
TBSPNDCTBuilder: adds nested dissection to the standard BSP,
TBSPPartCTBuilder: allows a user defined first partitioning step, e.g. the first level of the cluster tree is defined by the user,
TBSPGroupCTBuilder: performs standard BSP but groups individual indices, i.e. each index is assigned to a group and partitioning is done with respect to the groups instead of indices, ensuring that all indices in the same group end in the same cluster.

The first two algorithms, e.g. TBSPCTBuilder and TBSPNDCTBuilder, are usually the default methods to choose for clustering. To compute inner boundaries, TBSPNDCTBuilder needs additional information besides the coordinates, describing their connectivity. This is supplied by a sparse matrix (TSparseMatrix), where nonzero entries are used to identify a connection between indices.

autoptr< TSparseMatrix >  S;
// ... fill sparse matrix 
TBSPNDCTBuilder          ct_builder( S.get(), & part_strat );
autoptr< TClusterTree >  ct( ct_builder.build( coord.get() ) );

There is an optional third argument 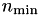$n_{\min}$ to TBSPNDCTBuilder, and also to all other constructing methods, which defines a lower boundary for leaves in the cluster tree, e.g. a node with less than 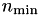$n_{\min}$ indices will not be further divided. Standard values are in the range of 20 or 40.

TBSPPartCTBuilder and TBSPGroupCTBuilder can be considered to represent two ends of a spectrum: the first algorithm can be used to divide indices explicitly whereas the second ensures that indices are not divided. In pactise however, TBSPPartCTBuilder is usually chosen, if the user has a predefined block system where the block structure shall be incorporated into the 𝓗-structure.

The following example puts every even index into the first block and all odd indices into the second one. The initial partition is hereby described by an array (std::vector) with the same size as the number of indices and the value at position i defines the block index i should belong to.

std::vector< idx_t >  partition( nindices );
for ( size_t  i = 0; i < nindices; ++i )
    partition[i] = ( i % 2 );
TAutoBSPPartStrat        part_strat( coord.get() );
TBSPCTBuilder            ct_builder( & part_strat );
TBSPPartCTBuilder        part_ct_builder( partition, & ct_builder );
autoptr< TClusterTree >  ct( part_ct_builder.build( coord.get() ) );

TBSPPartCTBuilder uses a base cluster tree builder for further construction, i.e. after the first level. Here, any algorithm may be used.