void hlib_set_config       ( const char *             option,
                             const char *             value,
                             int *                    info );
void hlib_get_config       ( const char *             option,
                             char *                   value,
                             const size_t             len,
                             int *                    info );
void hlib_print_parameters ();

Please note, that the names and values correspond to the names and values of the environment variables and not of the C++ parameters.

HLIB::CFG::BLAS

Name	Type	Description	Default Value
`use_rrqr_trunc`	bool	use RRQR based truncate instead of SVD based	false
`use_double_prec`	bool	use double precision SVD for single precision types	false
`use_gesvj`	bool	use gesvj instead of gesvd/gesdd	false
`gesvd_limit`	idx_t	upper matrix size limit for using gesvd (gesdd for larger matrices)	1000
`check_zeroes`	bool	check for and remove zero rows/columns in input matrices of SVD	false
`check_inf_nan`	bool	check for INF/NAN values in input data	false

use_rrqr_trunc

Rank-revealing QR (RRQR) uses column pivoted QR to determine the numerical rank of a given matrix. This is used in 𝖧𝖫𝖨𝖡𝗉𝗋𝗈 to truncated low-rank matrices with respect to a given precision or rank. In contrast to the SVD based algorithm, RRQR does usually not compute a best approximate, which normally results in a larger rank of the low-rank matrices or reduced accuracy in case of a fixed rank. However, the RRQR algorithm is faster than SVD, which results in a better runtime of the ℋ-algorithm.

Please note, that this behaviour is strongly depended on the given ℋ-matrix. In extreme cases, the ℋ-arithmetic may be slower since the rank of low-rank matrices may be much higher compared to SVD.

use_double_prec

If 𝖧𝖫𝖨𝖡𝗉𝗋𝗈 is compiled with single precision value types, setting use_double_prec to true, results in using double precision for computing the SVD during truncation. This increases accuracy and may reduce memory due to more accurate rank estimates.

use_gesvj

LAPACK provides an additional SVD algorithm (gesvj), which is often more accurate compared to the standard algorithms (gesvd, gesdd). Especially for extreme cases, e.g., very small singular values, this may be a better choice. However, gesvj is slower compared to the other algorithms (usually a factor of two).

check_zeroes

The SVD based algorithm may have problems of the input matrix has zero rows/columns (more precise the LAPACK algorithms used by the truncation). To fix this, such rows/columns can be eliminated from the input matrices.

HLIB::CFG::Cluster

Name	Type	Description	Default Value
`nmin`	uint	upper limit for minimal block size	60
`split_mode`		default split mode during geometrical clusterung	`adaptive_split_axis`
`adjust_bbox`	bool	adjust bounding box during clustering to local indices and not as defined by parent partitioning	true
`cluster_level_mode`		permit block clusters with clusters from different levels or not	`cluster_level_equal`
`sync_interface_depth`	bool	synchronise depth of interface clusters with domain clusters in ND case	true
`sort_wrt_size`	bool	sort sub clusters according to size, e.g. larger clusters first	false

nmin

The optimal value for nmin depends on the given problem and what is to be optimised: memory or runtime. As a rule of thumb, the smaller nmin the less memory is used and the larger nmin the better the runtime.

The default value is chosen based on benchmarks for dense matrices. For sparse matrices a higher value is often better (nmin = 100 ... 300).

split_mode

When partitioning a given geometry using binary space partitioning (BSP), the split axis may be chosen regularly (regular_split_axis), i.e., cycling through x, y and z axis or adpative (adaptive_split_axis), i.e., choose the longest axis. Theory usually assumes regular splitting while adaptive splitting often results in a better (less memory, better runtime) partitioning.

adjust_bbox

During BSP the sub domains may be assigned a bounding box by splitting the bounding box of the parent domain along the split axis or by recomputing the bounding box based on the coordinate information of the indices in the corresponding sub domains. The latter method usually reduces bounding box sizes and leads to a coarser partitioning of the ℋ-matrix, which in practise is often more optimal (less memory, better runtime). However, theory usually assumes a non-adaptive bounding box.

cluster_level_mode

When building block clusters, i.e., a product of two clusters, normally only clusters of the same level are permitted to form block clusters. For some applications it may result in a better partitioning when also allowing clusters from different levels during block cluster tree construction (see also sync_interface_depth).

sync_interface_depth

If nested dissection is used, the depth of the interface tree is normally adjusted to the depth of the domain trees. For some applications, switching this off may result in a better partitioning (see also cluster_level_mode).

HLIB::CFG::Arith

Name	Type	Description	Default Value
`use_dag`	bool	use DAG based arithmetic	true
`abs_eps`	real	default absolute error bound for low-rank SVD	0
`recompress`	bool	recompress matrix after low-rank approximation	true
`use_zero_matrix`	bool	use special zero matrix type for domain-domain blocks	true
`build_ghost_matrix`	bool	build ghost matrices for remote blocks	false
`build_sparse_matrix`	bool	use sparse matrices during construction	false
`eval_type`		point-wise or block-wise evaluation of blocks	`block_wise`
`storage_type`		storage type of diagonal blocks in factorisation	`store_inverse`
`max_seq_size`	size_t	switching point from parallel to sequential mode	100
`max_seq_size_vec`	size_t	switching point for vector based operations	250
`coarsen_build`	bool	coarsen matrix during construction	false
`coarsen_arith`	bool	coarsen matrix during arithmetic	false
`check_cb_ret`	bool	check data returned by callback functions during construction	true
`arith_max_check`	uint	upper matrix size limit for addition tests during arithmetic	0

use_dag

For multi and many core chips, the DAG based ℋ-arithmetic is able to utilise the CPU resources much better than the classical recursive algorithms. Only for sequential computations, a slightly better runtime may be possible with the recursive approach due to overhead for DAG based computations.

abs_eps

Singular values smaller than abs_eps are removed from the resulting matrix during truncation independent on the given accuracy or rank.

recompress

The low-rank approximations computed during ℋ-matrix construction may not be optimal with respect to the rank. A recompression using SVD (or RRQR) may reduce the rank and hence memorr without affecting accuracy.

use_zero_matrix

When using nested dissection, off-diagonal domain-domain blocks remain zero during ℋ-LU factorisation. A special matrix type can therefore be used to signal this property to the ℋ-arithmetic and to improve performance of the algorithms.

However, make sure that only such ℋ-algorithms are used, which preserve the zero property. Otherwise, an error may occur.

eval_type

The evaluation type affects the handling of diagonal leaf blocks. Either factorisation is also performed for such blocks (point_wise) or the blocks are handled as a full block using inversion (block_wise). The latter has several advantages, e.g., permits limited pivoting during inversion and increases performance due to better cache utilisation (BLAS level 3 functions).

storage_type

When computing matrix factorisations, the diagonal leaf blocks may store either the actual result of the factorisation (store_normal) or the inverse of such blocks (store_inverse). Since for evaluation of the inverse operators, either during factorisation or during matrix-vector multiplication, the inverse if the matrix blocks is needed, storing the inverse results in better performance.

However, if also the original matrix should be evaluated using the factorised form, normal storage may be more optimal in terms of runtime.

max_seq_size (_vec)

Matrices smaller than max_seq_size are handled by ℋ-arithmetic sequentially since this is more efficient compared to parallel handling. Same holds for max_seq_size_vec in case of matrix-vector operations.

HLIB::CFG::Solver

Name	Type	Description	Default Value
`max_iter`	uint	maximal number of iterations	100
`rel_res_red`	real	relative residual reduction, e.g., stop if 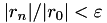$\|r_n\| / \|r_0\| < \varepsilon$	1e-8
`abs_res_red`	real	absolute residual reduction, e.g., stop if 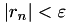$\|r_n\| < \varepsilon$	1e-14
`rel_res_growth`	real	relative residual growth (divergence), e.g., stop if 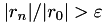$\|r_n\| / \|r_0\| > \varepsilon$	1e6
`gmres_restart`	uint	restart for GMRES iteration	20
`initialise_start_value`	bool	initialise start value before iteration	true
`use_exact_residual`	bool	compute exact residual during iteration	false

rel_res_growth

This parameter stops the iteration in case of divergence.

initialise_start_value

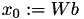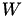Normally, the start value of the iteration is initialised as $x_0 := W b$ with $W$ being the preconditioner. In case of a good (or very good) preconditioner, e.g., 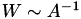$W \sim A^{-1}$ , this may eliminate iteration at all.

However, if the user has a good guess for the start value this behaviour may be switched off.

use_exact_residual

Most iterations approximate the residual norm during computations. Especially in the preconditioned case, this may result in a large deviation from the real residual norm. At the expense of one (unpreconditioned case) or two (preconditioned case) additional matrix-vector multiplications, the exact norm is computed instead.

HLIB::CFG::BEM

Name	Type	Description	Default Value
`quad_order`	uint	default quadrature order	4
`adaptive_quad_order`	bool	use distance adaptive quadrature order	true
`use_simd`	bool	use special vector functions if available	true
`use_simd_sse3`	bool	use special SSE3 vector functions if available	true
`use_simd_avx`	bool	use special AVX vector functions if available	true
`use_simd_avx2`	bool	use special AVX2 vector functions if available	true
`use_simd_mic`	bool	use special MIC vector functions if available	true

quad_order

For the evaluation of the bilinear forms a quadrature rule is used for which the default order is defined with this parameter. For high accuracy ℋ-arithmetic, a higher order may be used, e.g., 5 or 6.

adaptive_quad_order

For far-field evaluation, the quadrature order may be reduced for normal bilinear forms, resulting in much reduced runtime.

use_simd

All implemented bilinear forms have special implementations using SIMD instructions of the CPU. Normally, this results in a faster computation compared to compiler generated code. So, in most cases this flag is only needed for comparison or for debugging.

HLIB::CFG::IO

Name	Type	Description	Default Value
`use_matlab_syntax`	bool	use Matlab syntax for printing complex numbers, vectors and stdio	off
`color_mode`		use color in terminal output if supported	true
`charset_mode`		use ascii or unicode in normal terminal output	depends on terminal

Table of Contents