|
HLIBpro
2.5.1
|
𝖧𝖫𝖨𝖡𝗉𝗋𝗈 implements several solvers for linear equation systems
![\[ Ax = b \]](form_296.png)
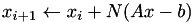 with iteration matrix
with iteration matrix 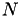 ,
,All solvers have the same interface function for solving the given system:
Here, W is an optional operator used as a (left) preconditioner for solving the equation system. Furthermore, info is an optional object for storing information about the iteration process, e.g., if converged, residual norm or convergence rate.
Assuming a given matrix object A and vectors x and y, the minimal solving code looks as
20 for GMRES defines the restart of the method, e.g., the dimension of the local Krylov subspace.By default, the initial guess 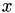 is initialized to some solver dependent value before the iteration. To disable this, you may use the function
is initialized to some solver dependent value before the iteration. To disable this, you may use the function initialise_start_value:
Since not all solvers are suitable for all matrices, e.g., not applicable for unsymmetric matrices, TAutoSolver decides which solver to use for a given combination of matrix and preconditioner.
The iteration process is controlled using objects of type TSolver::TStopCriterion. The following parameters may be used to define the stop of the iteration:
max_iter: maximal number of iteration steps,abs_res_reduct: absolute residual norm (often also called tolerance), i.e., stop if 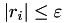 ,
,rel_res_reduct: relative residual norm with respect to initial residual, i.e., stop if 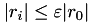 ,
,rel_res_growth: relative residual growth, i.e., stop if 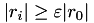 (in case of divergence).
(in case of divergence).All parameters may be specified while construction TStopCriterion objects:
However, resonable default values are set.
To obtain more information of the solution process, an object of type TSolverInfo has to be provided to the solve function. Afterwards, the following function may be used to gather the corresponding data:
has_converged() : did the iteration converge,has_diverged() : did the iteration diverge (bases on TStopCriterion),has_failed() : did the iteration failed, e.g., due to breakdown,n_iter() : return number of iteration stepsconv_rate() : return convergence rate,res_norm() : return norm of residual after iteration stopped.During construction of TSolverInfo, one may also specify to store the complete iteration history and to print this data during iteration:
Beside various solvers, 𝖧𝖫𝖨𝖡𝗉𝗋𝗈 also implements different preconditioning techniques for the iteration methods.
Of course, the most important of these preconditioners is based on some form of matrix inversion using ℋ-arithmetic, e.g., ℋ-LU factorization, ℋ-WAZ factorization of ℋ-inversion. Simply provide the corresponding linear operator object to the solve function:
 is modified during factorization.
is modified during factorization.Beside ℋ-based methods, 𝖧𝖫𝖨𝖡𝗉𝗋𝗈 also implements some classical preconditioners:
 , with
, with 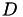 being the (block) diagonal of
being the (block) diagonal of 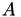 .
.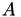 .
.However, the point-wise Gauss-Seidel and SOR methods may only be used (and only make sense) when using a sparse matrix (TSparseMatrix). For a ℋ-matrix, only block-wise methods are available for Gauss-Seidel.
In case of Jacobi, both, point- and block-wise may be used for all matrix types. Furthermore, it also allows to define the size of the diagonal blocks.
The example above using a block-wise Gauss-Seidel precondtionier would look like: